python x シミュレーション | モンテカルロシミュレーションを用いて円周率「π」を求めよう!
- 2023.04.15
- Python

今回はアルゴリズムの一つ「モンテカルロ法」について取り上げます。
モンテカルロ法とは?
モンテカルロ法とは、ランダムな数値を用いて、数値計算を行う手法のことです。
モンテカルロ法は、確率的に求めることが困難な問題や、数式的に解くことが困難な複雑な問題に対して、数値的な解法を提供することができます。
よくある事例:円周率(π)を求めてみよう
例えば、円周率(π)を求める問題を考えてみましょう。
πを求める過程
以下のような図形を用意します。
・1辺が「2r」の正方形
・半径が「r」の円
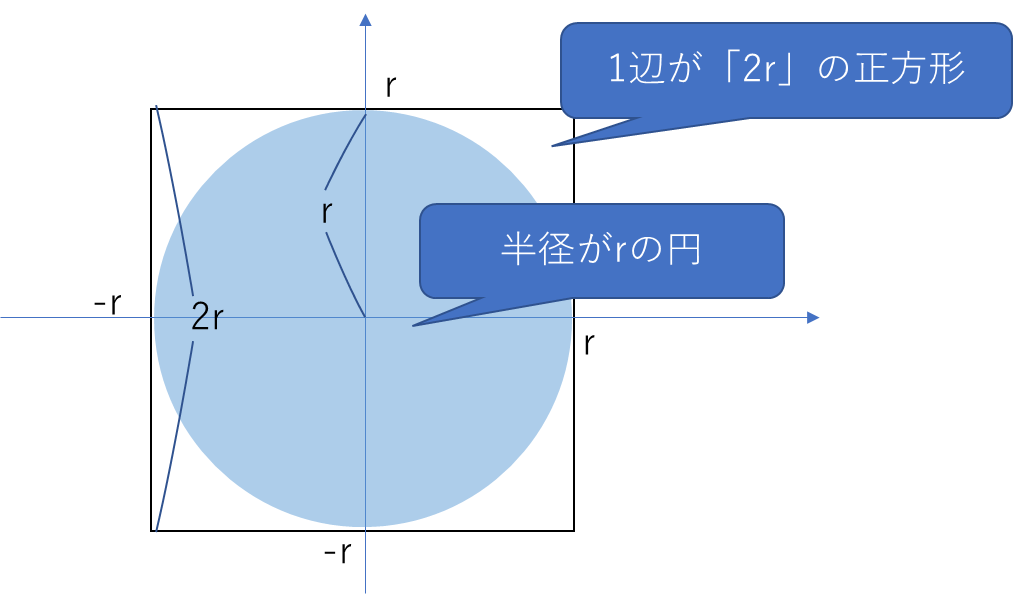
それぞれの面積は以下のようにあらわすことができます。
※円の面積は便宜上「π」を使っていますが、この時点では値が分かっていないものとしています。

上記の面積より、πは以下のようにあらわすことができます。
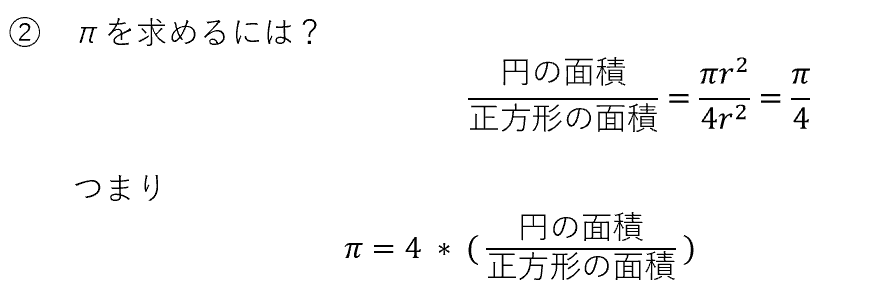
πは円の面積と正方形の面積が分かれば求めることが出来そうです。
しかし、今の時点では「円の面積はπを用いない」と求めることができません。
そこで「モンテカルロ法」を用いることとします。
1)正方形の中にランダムに大量の点を落とします。
2)正方形を埋め尽くすほどの点を落としたとき、
【円内に落ちた点の数≒円の面積】
とみなすことができます。
3)つまり、以下のような式が成り立ちます。

4)点の数が多いほど、πの値の精度が高まります。
以上がモンテカルロ法を用いた、πの推定方法となります。
pythonを用いたシミュレーション
では、実際にPythonでシミュレーションしてみましょう!
以下がコードです。
import random
import matplotlib.pyplot as plt
# シミュレーション回数
num_simulations = 1000000
# 円内に入った点の数をカウントする変数
num_points_inside_circle = 0
# シミュレーション結果を保存するリスト
x_inside_circle = []
y_inside_circle = []
x_outside_circle = []
y_outside_circle = []
# num_simulations回シミュレーションを実行する
for i in range(num_simulations):
# 正方形内のランダムな座標を生成
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# 原点からの距離を計算
distance = x ** 2 + y ** 2
# 距離が1以下の場合、円内にあるとみなしてカウントする
if distance <= 1:
num_points_inside_circle += 1
x_inside_circle.append(x)
y_inside_circle.append(y)
else:
x_outside_circle.append(x)
y_outside_circle.append(y)
# 円周率を計算
pi = 4 * num_points_inside_circle / num_simulations
# 結果を出力
print("円周率の近似値: ", pi)
# 円周率のシミュレーション結果を描画
fig, ax = plt.subplots()
ax.set_aspect('equal', adjustable='box')
circle = plt.Circle((0,0), 1, fill=False)
ax.add_artist(circle)
ax.scatter(x_inside_circle, y_inside_circle, s=1, color='blue')
ax.scatter(x_outside_circle, y_outside_circle, s=1, color='red')
plt.show()
以下が結果です。
点の数を100~100,000まで増やしてシミュレーションしています。
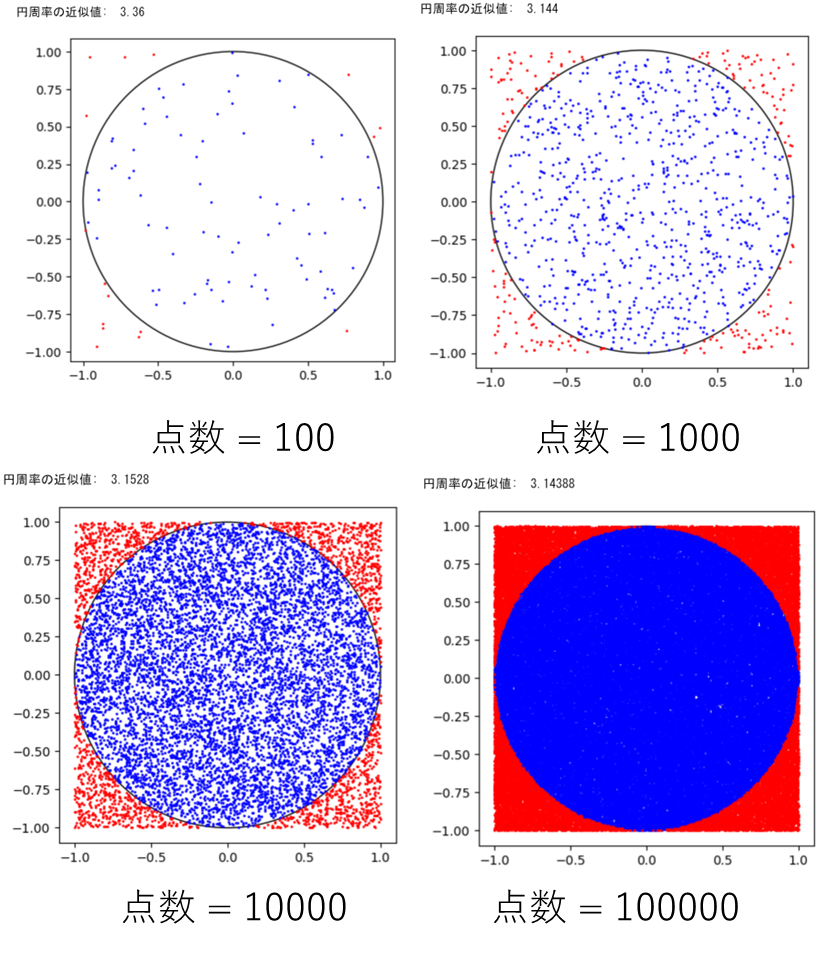
このように、モンテカルロ法は、ランダムな数値を用いて、問題を解決する方法です。
確率的な問題や複雑な問題に対して有効な手法であり、様々な分野で利用されています。
今回は以上です!ではまた!
-
前の記事

Google Colab | Python で LINE Notify から画像やスタンプを送る方法 2023.02.25
-
次の記事

python x ソートアルゴリズム | バブルソートで並び替えよう!〜アルゴリズムとデータ構造 2023.04.15

